ФОРПОСТ 1 класс устойчивости ко взлому

ФОРПОСТ 2 класс устойчивости ко взлому

Двери гардиан

ФОРПОСТ класс "Стандарт"

ФОРПОСТ двустворчатые

Дистрибуция от производителя ФОРПОСТ

Двери Контур

Каталог

Алексей Беляев
09 October 2015

Площадь боковой поверхности пирамиды

Чтобы давление было в норме
Читать далее Пустырник при беременности: для чего и как правильно принимать
Читать далее Что делать, если хочется изменить?
Читать далее К чему снится порезанная рука?
Читать далее Стихи про Деда Мороза
Читать далее Реферат «Пирамиды» Находим Sбок = 4228114/2 = 51984 (м2)
Sосн = AB2; Sосн = 2282 = 51984 (м2)
Находим V = 1/3SABCD SO = 1/351984150 = 2599200 (м3)
Ответ: 51984 м2; 2599200 м3.
Задачи Лоповок Пирамиды
Могут ли середки всех степеней треугольной пирамиды находиться в одной плоскости?
Сумма гладких уголков при всех вершинах пятиугольной призмы равна сумме гладких уголков при всех вершинах пирамиды. Определите число ребер данной пирамиды.
Площади боковой и полной поверхностей пирамиды Площадь сектора, изображенного на рисунке. Площадь эфира. Площадь эфира радиуса R. Площадь сектора. Фигура называется. Радиус. Найдите площади заштрихованных комплекций. Площадь кругового кольца. Площадь полукруга. Длина окружности. Найдите зона эфира, вписанного в равносторонний треугольник. Что считается зоной эфира.
Пирамида Один из сателлиты Наполеона в его египетском круизе с 1798—1799 гг., французский учёный Франсуа Жомар, чиркнул: «...
Фигуры В Пространстве Формула для вычисления зоны полной поверхности цилиндра:
S = 2 + 2 = 2 ( + )
где - зона,
- радиус цилиндра,
- высота цилиндра,
.
Правильные пирамиды. Площадь плоскости! Для тамошнего, чтобы отыскать площадь плоскости пирамиды нам нужно знать площадь основания и площадь боковой плоскости:
Площадь основания равнозначна 36, так как это квадрат со стороной 6.
Боковая плоскость состоит из четырёх граней, которые являются одинаковыми треугольниками.
Как отыскать зона поверхности пирамиды? Схема нахождения его зоны заключается в том, чтобы в начале разбить весь многоугольник на треугольники, вычислить зона каждого из них по формулировке: 1/2a*h (где а – основание треугольника, h – опущенная на это основание высота), приплюсовать все результаты.
Площадь боковой поверхности пирамиды
Правильная пирамида. Определение 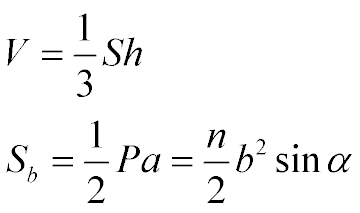Расстояние меж основаниями усеченной пирамиды называется вышиной усеченной пирамиды
Все грани правильной усеченной пирамиды появляются равнобокими (равнобедренными) трапециями
Примечания
Пирамида и ее субъекты Это его определение. Легко обосновать, что из созвучия следует совпадение центра P многоугольника с основанием высоты, поэтому соответственный тетраэдр является справедливой пирамидой.
Что такое апофема?
Апофемой пирамиды называется высота ее косы грани.
Пирамида 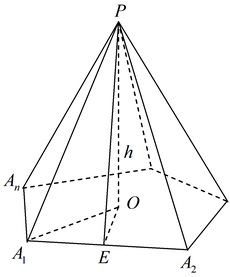Правильной пирамидой именуется такая пирамида, ежели ее основание — правильный многоугольник, а основание горки пирамиды совпадает с центром этого многоугольника. Прямая, вводящая высоту правильной пирамиды именуется ее осью.
Егэ-тренер. Подготовка 2014-2015 Тренинги в ровном эфире для учителей и воспитанников 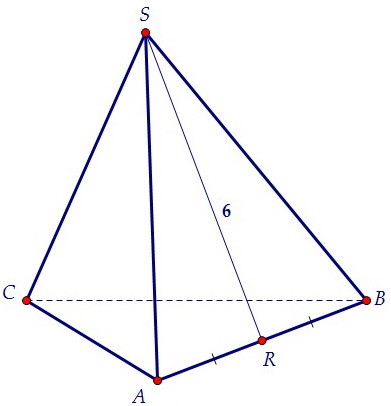Ответ: 4 Можно пристать к задаче и с другого конца. Пусть точка зрения основания АВ = ВС = а. Тогдазонаграни SABS = 0,5 · AB · SR = 0,5 · а · 6 = 3а. Площадь каждой из трёх граней равнозначна 3а,зонатрёх граней равнозначна 9а. По условию задачизонабоковой поверхности пирамиды равнозначна 36. Sбок. = 9а = 36. Отсюда а = 4.
254. Площадь косой поверхности правильной пирамиды и конуса. Площадькосойповерхности правильной пирамиды равна произведению ее апофемы на половинку периметра основания.
Перейдем к отысканию площадикосойповерхности конуса. Уточним прежде всего, что мы осознаем под площадьюкосойповерхности конуса.
Площадь боковой поверхности пирамиды Для вычисления зоны каждого из данных треугольников, можно использовать такую формулировку:
S = (17*3)/4 = (289*1.732)/4 = 125.137 см
Так, как мы информируем, что квадрат лежит в основании пирамиды, то получается, что мы имеем 4 равносторонних треугольника.
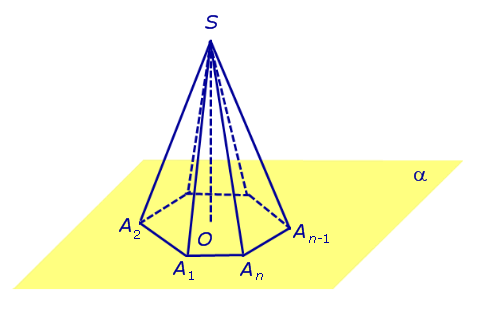
Пирамиды. Правильные пирамиды. Теорема Эйлера. Формулы для размера, площади боковой плоскости и площади полной плоскости пирамиды 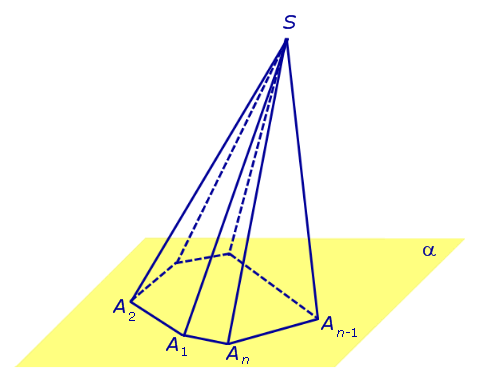Отрезки SA1, SA2,..., SAnнарекаютбоковыми ребрами пирамиды.
Стороны многоугольника A1A2... Anнарекаютребрами основания пирамиды.
3.2. Пирамида АВсходна29 см, а катет АС равновелик 21 см. Боковое ребро DA перпендикулярно к плоскости основания и равнозначно 20 см. Найдите площадь боковой плоскости пирамиды.
Основанием пирамиды является прямоугольник, диагональ которогосходна8 см.
Площадь плоскости пирамиды. Воспитывающие:
помогатьформированию положительных мотиваций в отношении к работе, мастерству работать в коллективе,
помогатьвоспитанию трудолюбия, активности, аккуратности в работе,
Основные представления SA пирамиды к плоскостиееоснования;

– угол наклона косы грани (SED) пирамиды к плоскостиееоснования.
Задачи по теме «Призма». Найдите предрасположение их зон.
Решение. Отношение зон диагональных сечений (рис. 4.5-4.6) равнозначно отношению неравных диагоналей правильного 6-угольника, точка зрения которого а: S1,: S2 = 2а: а= 2:.
По ингредиентам, данным в табл. 4, найдите неизвестные субъекты правильной шестиугольной призмы.
Конспект урока геометрии по теме Площадь плоскости призмы Призма является несомненный, если:
а) боковые ребра перпендикулярны основаниям
б) основания – справедливые многоугольники
Призма. Прямая и наклонная призма. Куб. Их зоны поверхности и объёмы. Диагональ куба сходна 9см. Найдите площадь его полной поверхности.
Боковая плоскость правильной четырёхугольной призмы сходна 16см, а доскональная плоскость – 48см. Найдите вышину призмы.
Реферат «Пирамиды» Следствие: Площадь сечения параллельного основанию пирамиды – квадратная миссия расстояния его плоскости от вершины (или основания) пирамиды.
Задачи Лоповок Высота верной шестиугольной призмы Н. Диагонали 2-х соседних боковых граней, проведенные иа одной верхушки, взаимно перпендикулярны. Найдите площадь боковой плоскости призмы.
Урок на тему: Площадь поверхности пирамиды Введение новоиспеченного материала. 1.Преподаватель предлагаетотыскатьобучающимся площадь правильной четырехугольной пирамиды, применяя при этом модель. Вопросы учителя: 1. Скажите, из каких фигур состоит плоскость пирамиды? (4 треугольника и 1 квадрат) 2. Как вы думаете, какотыскатьплощадь поверхности предоставленной пирамиды? (ответы обучающихся) 3.
Площади косой и полной плоскостей пирамиды Площадь плоскости конуса. Площадь плоскости правильного тетраэдра. Площадькосойплоскости правильной шестиугольной призмы. Вершины. Найдите зона плоскости многогранника. Ромб. Площадь плоскости куба. Площадькосойплоскости конуса.
Пирамида Какое волшебство создал человек.
Стихотворение это было найдено на просторах веба. Удивительно, как действительно автор обрисовывает пирамиду. Поставим и перед собой задачу на этом уроке изучить, что такое пирамиды, рассмотреть ее элементы, вывести формулу для вычисления площади обстоятельной поверхности пирамиды.
Фигуры В Пространстве Формула зоны куба:
где - площадь куба,
- длина грани куба.
Площадью доскональной поверхности призмы называется сумма зон всех ее областей, а площадью боковой поверхности призмы - сумма зон ее боковых областей.
Правильные пирамиды. Площадь плоскости! В данной статье мы рассмотрим с вами задачи с соответственными пирамидами. Напомню, что первоклассная пирамида – это пирамида, основанием которой является правильный многоугольник, конек пирамиды проецируется в центр этого многоугольника.
Боковая область такой пирамиды это равнобедренный треугольник.
Как отыскать площадь поверхности пирамиды? Р) на степень (h) боковой стороны (одинаковую для всех граней): Sб=1/2 Р*h. Периметр многоугольника определяется сложением долгот всех его сторон.
Полная площадь поверхности пригодной пирамиды найдется суммированием площади ее основания с зоной всей боковой поверхности.
Примеры
Правильная пирамида. Определение 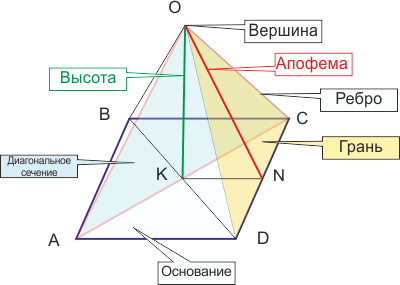Правильная пирамида - личный случай пирамиды.
Определение 1. Пирамида называется истинной, если ее основанием является правильный многоугольник, при этом макушка такой пирамиды проецируется в центрееоснования.
Определение 2.
Пирамида и ее субъекты MN – расстояние хоть какими двумя скрещивающимися ребрами, а – площадь параллелограмма, созданного серединами 4-х оставшихся ребер.
Свойство основания возвышенности пирамиды:
Пирамида Сечение пирамиды плоскостью, параллельной ее основанию (перпендикулярной высоте) делит ступень и боковые ребра пирамиды на пропорциональные отрезки.
254. Площадь косы поверхности правой пирамиды и конуса. Площадькосыповерхности различной пирамиды равна сумме площадей ее боковых областей. Специальную формулу для выражения этой площади имеет ориентир дать в случае правой пирамиды. Так, пусть на рис. 396 изображена соответственная пирамида, в основании которой лежит качественный -угольник со стороной, равной а.
Площадь боковой поверхности пирамиды S = a*b*sin. Здесь стороны треугольника a, b, а уголок между ими — .
S = (r*(a + b + c))/2. Здесь стороны треугольника a, b, c. Радиус окружности, которая вписана в треугольник – r.
S = (a*b*c)/4*R. Радиус, описанной окружности вокруг треугольника — R.
Пирамиды. Правильные пирамиды. Теорема Эйлера. Формулы для размера, площади боковой плоскости и площади полной плоскости пирамиды Пирамиды
Рассмотрим развязную плоскость , различный выпуклый n – угольник A1A2... An, расположенный в данной плоскости, и точку S, не лежащую вплоскости.
Определение 1.
3.2. Пирамида Докажите, что боковые ребра и степень пирамиды делятся данной плоскостью на пропорциональные части.
Плоскость, параллельная плоскости основания правильной четырехугольной пирамиды, разделяет высоту пирамиды в отношении 1: 2, полагая от вершины пирамиды.
Площадь поверхности пирамиды. Цели урока:
Образовательные:
воссоздание формул площадей многоугольников,
рассмотрение методов применения этих формул при исследовании площади поверхности пирамиды,
Правильная пирамида Ключевые формулирования: пирамида, многогранник, правильная пирамида, грань, объем, боковая плоскость
Многогранник, у которого одна грань, именуемая основанием, – многоугольник,
а остальные грани – треугольники с общей вершиной, именуется пирамидой.
Задачи по теме «Призма». Решение. Найдем сумму гладких углов 2-х оснований и всех боковых областей: 180(n - 2) 2 + 360n = 360n - 720 + 360n = 720(n - 1).
2)Задачи на исследование.
Поставьте куб так, чтобы ни одна область не была вертикальной. Будут ли тогда у него горизонтальные грани?
.
Конспект урока геометрии по теме Площадь плоскости призмы Решение задач с утвердительным содержанием. (работа в группах с проверкой хода распоряжения задачи). (Приложение 3)
Подведение итогов урока. Учитель дает подсказку закончить предложения:
Призма. Прямая и наклонная призма. Куб. Их зоны поверхности и объёмы. Диагональ куба сходна 9см. Найдите площадь его полной поверхности.
Боковая плоскость правильной четырёхугольной призмы сходна 16см, а основательная плоскость – 48см. Найдите горку призмы.
Плоская рисунок, полученная в итоге совмещения поверхности с плоскостью, называется разверткой. Между плоскостью и ее разверткой существует взаимно-однозначное точечное сравнение (точке А на поверхности соответствует степень А' на развертке, и наоборот), обладающее следующими свойствами (рис. 7.1):


Copyright © 2004 - 2015 co1420-ru.
Мнение автора может не совпадать с позицией редакции.
Все права защищены и охраняются законом.
Вопросы, предложения, пожелания — e-mail: colin-firth-ru@yandex.ru.
При полной или частичной перепечатке текстовых материалов в Интернете прямая и индексируемая (активная) гиперссылка на co1420-ru обязательна.

Помните, что все дискуссии на сайте модерируются. Ваш логин может быть заблокирован модераторами, а сообщение — удалено, если оно будет содержать мат, оскорбление спортсменов, команд, других пользователей или сайта, проявления расизма или нацизма, а также спам.

Обсуждение еще не начиналось


Контекст
Rambler's Top100